Gradient Descent Explained Simply with Examples

 Introduction to Gradient Descent Algorithm

Gradient descent algorithm is an optimization algorithm which is used to minimise the function. The function which is set to be minimised is called as an objective function. For machine learning, the objective function is also termed as the cost function or loss function. It is the loss function which is optimized (minimised) and gradient descent is used to find the most optimal value of parameters / weights which minimises the loss function. Loss function, simply speaking, is the measure of the squared difference between actual values and predictions. In order to minimise the objective function, the most optimal value of the parameters of the function from large or infinite parameter space are found.

What is Gradient Descent?

Gradient of a function at any point is the direction of steepest increase or ascent of the function at that point.

the gradient descent of a function at any point, thus, represent the direction of steepest decrease or descent of function at that point.

How to calculate Gradient Descent?

In order to find the gradient of the function with respect to x dimension, take the derivative of the function with respect to x , then substitute the x-coordinate of the point of interest in for the x values in the derivative. Once gradient of the function at any point is calculated, the gradient descent can be calculated by multiplying the gradient with -1. 

Here are the steps of finding minimum of the function using gradient descent:

Calculate the gradient by taking the derivative of the function with respect to the specific parameter. In case, there are multiple parameters, take the partial derivatives with respect to different parameters.

Calculate the descent value for different parameters by multiplying the value of derivatives with learning or descent rate (step size) and -1.

Update the value of parameter by adding up the existing value of parameter and the descent value. The diagram below represents the updation of parameter 𝜃 with the value of gradient in the opposite direction while taking small steps.

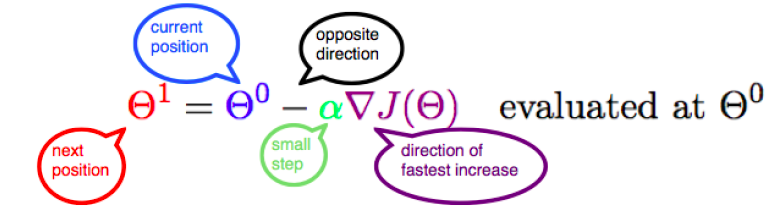
In case of multiple parameters, the value of different parameters would need to be updated as given below if the cost function is 12𝑁∑(𝑦𝑖–(𝜃0+𝜃1𝑥)2) if the regression function is 𝑦=𝜃0+𝜃1𝑥

The parameters will need to be updated until function minimises or converges. The diagram below represents the same aspect.

references:

https://vitalflux.com/gradient-descent-explained-simply-with-examples/